【圆周角定理】

看下面的图片。

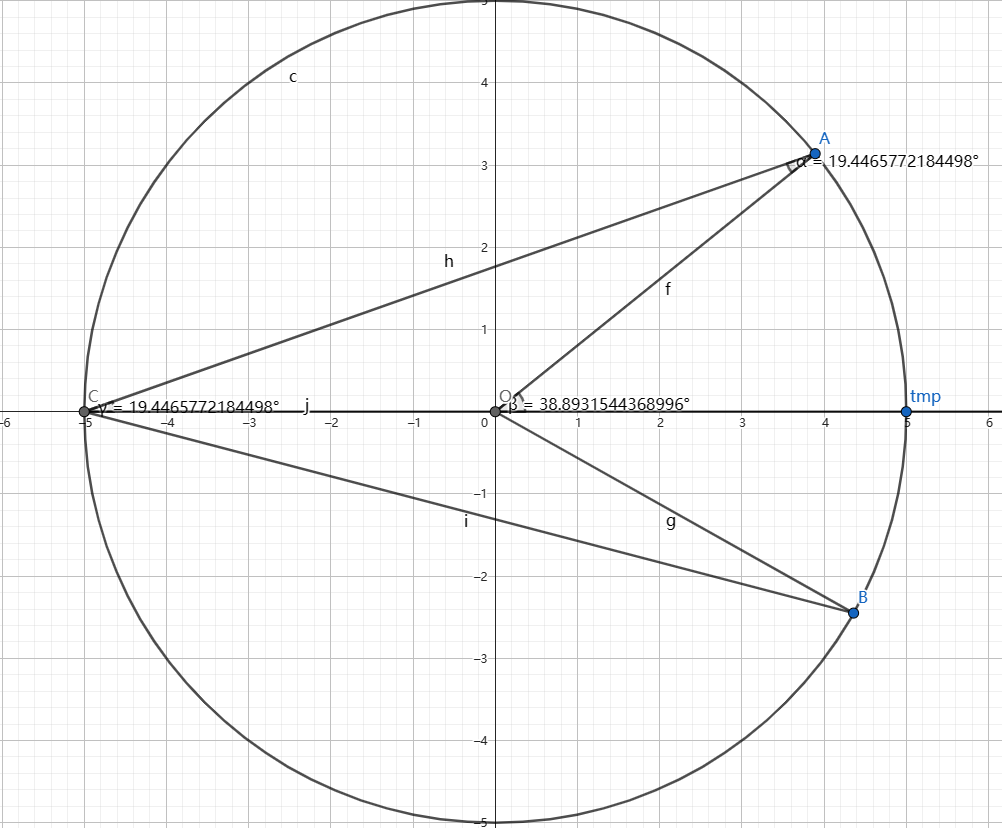
定理是在圆周上的任意一点 $C$ 满足 $\angle AOB = 2\angle ACB.$

为什么呢？首先考虑线段 $AC ,BC$ 与 $AO,BO$ 两两之间没有交点的情况。

作 $CO$ 的延长线。

由外角定理，$\beta = \alpha + \gamma.$ 而 $OA=OC =R,$

$\therefore \alpha = \gamma,$

$\therefore \beta = 2\gamma.$

另外两种情况同理。请读者自己证明，不是笔者懒惰。

【圆周角定理的推论】

过圆心的直线，它与圆相交两点，这两点与圆上的一点所形成的角一定是直角。

将上面的 $\angle AOB = 180^{\circ}$ 也就是平角带入进去就好了。这一点在下面证明正弦定理的时候同样有效。

【正弦定理】

那么有我来证明一下正弦定理吧。

已知：对于 $\triangle ABC,$ $a,b,c$ 分别为 $\angle A ,\angle B ,\angle C$ 的对边。 $R$ 为 $\triangle ABC$ 的外接圆半径。

求证：有 $\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R.$

如图所示：

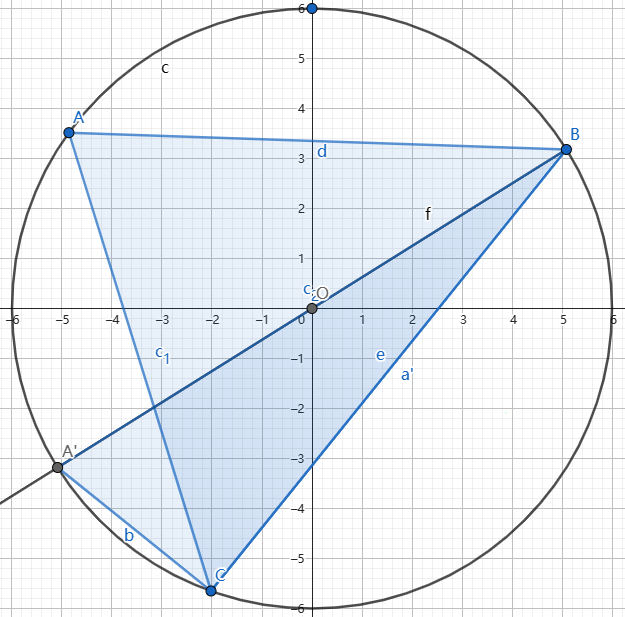
由于 $A'B$ 经过圆心，所以 $\angle A'CB = 90^{\circ}.$

显然，$2R=A'B.$

$\therefore$ $a'=2R \sin A$

原式可化为 $\dfrac{2R \sin A}{\sin A}=2R$ ，由于三角形 $\triangle ABC$ 中 $\sin A \not = 0,$

$\therefore$ 原式两边同除以 $\sin A.$

$2R=2R$ 显然成立。

命题得证。